Tag: Additive Manfuacturing

PySLM Release – Version 0.6

3D Printing Additive Manufacturing Blog PySLM No Comments

After a long period, PySLM version 0.6 is released. This coincides with the intensity of commitments as a new academic at the University of Nottingham over the past year. The release has mainly focused on improvements and enhancements to the underlying codebase rather than the addition of entirely new features. There are several substantial changes to the underlying dependencies that contributes some improvements and performance throughout which PySLM users will benefit from.

Dependency changes

With the release of ClipperLib2 library, additional python bindings were exposed and released as a separate library in the PyClipr. These were created using the PyBind11 headers and provides the core functionality required to performing offsetting and clipping of path segments and hatch vectors. There are no substantial feature improvements inherited from the change, but a noticeable performance improvement can be observed. Another benefit is that PySLM does not require compilation via cython and is now a full source distribution available via PyPi repositories.

Another significant dependency change is the use of the manifold mesh Boolean library. This offers a substantial improvement to mesh manipulation operations, that are fundamental to successful support generation for use in metal L-PBF. The library provides robust intersection of water-tight meshes, that is also computationally efficient when compared to the prior PyClipr library which was based on the clipr library from over a decade ago. This significantly improves the quality of the volumes generated in BlockSupportBase and those derived from these such as those with the GridTrussSupport that provide perforations and teeth for metal L-PBF. Additionally, this removes an additional dependency that requires maintenance by myself, and is more cross-platform that what can be offered by the previous PyClipr library.

Further incremental changes, that will not affect users is migration to the Shapely 2.0 library and also Trimesh 4.0, which required some internal changes to maintain compatibility.

Support Generation Improvements:

The support generation has been improved to be more robust and reliable compared to the initial release in version 0.5.0. Further robustness checks are implemented in the ray-tracing method developed in version 0.5, for identifying correctly the support projection height maps which are used to identify boundaries of the support volume. Further use has been explored in applied research by TWI – see open access paper (An Interactive Web-Based Platform for Support Generation and Optimisation for Metal Laser Powder Bed Fusion) by Dimopoulos et al.

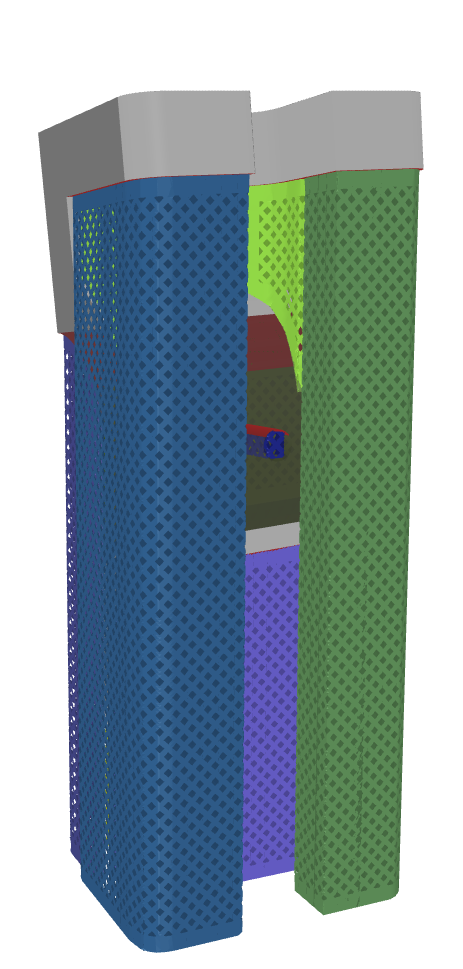
By default all BlockSupport‘s have smoothed boundaries by the use of spline fitting, which was previously only applied on self-intersecting supports. Smooth boundaries significantly improve the quality of the final GridBlockSupport, because the perforated grid truss skin can more smoothly conform to the boundary of the support volume.


Smoothed boundaries generated for all SupportVolumes for a complex part: including both self-intersecting supports and those only connected to the build-plate

As a recommendation to users, care must be taken to not smoothen the boundaries too much or these will not correctly conform to the original geometry causing the ray-projection algorithm to fail. A recommending starting point for the spline simplification factor is between 5-30, but is dependent on the relative part scale. Coinciding with the use of the manifold3d library, there is an appreciable improvement in the speed for generating the support volumes.

Another improvement is the more configurable parameters for Grid Truss Support generation. This includes further enhancement and control over the perforated teeth, across both upper and lower support volume surfaces. These are fully customisable by a user function, which ensure that a repeating shape is conformed in 3D across the surface profiles of the support volume.

Finally, a significant enhancement is correctly pre-sorting the scan vectors within the sliced support regions to take advantage of the line segments when scanning by the beam source. This significantly improves build productivity by minimising jumps across adjacent segments and ensures that the galvo-mirror movement remains mostly in the same direction.

A layer showing the order of scanning across all grid truss support generated for a complex topology optimised part. Jump distance is a total of 2056 mm with a total scan vector length 1377 mm.

Documentation Improvements

Further improvements to the inline documentation have been included alongside improvements and examples that are now provided on readthedocs. These provide basic information and guides for using PySLM, some of which is consolidated from these blog entries to aid new users using the library. Over time these will be further enhanced and amended to support researchers and users wishing to use PySLM in their work.

Conclusions & Change Log

The release has taken a while to release, but overall has received a level of polish and refinement that helps the release find use amongst more in commercially vested R&D projects and academic research. There are other developments still in the pipeline but much focus was on providing a long-term stable release for users. The full changelog can be found here.

Pyclipr – Python Polygon Clipping and Offsetting Library

3D Printing Additive Manufacturing Blog PySLM 1 Comment

Pyclipr is a Python library offering the functionality of the Clipper2 polygon clipping and offsetting library and are built upon pybind . The underlying Clipper2 library performs intersection, union, difference and XOR boolean operations on both simple and complex polygons and also performs offsetting of polygons and inflation of un-connected paths. Unfortunately, the contracted name (Clipr) is the closest name to that of the previous form.

Unlike pyclipper, this library is not built using cython, which was previously integrated directly into PySLM with custom modifications to provide ordering of scan vector. Instead the full capability of the pybind binding library is exploited, which offers great flexibility and control over defining data-structures. This library aims to provide convenient access to the modifications and new functionality offered by Clipper2 library for Python users, especially with its usage prevalent across most open source 3D Printing packages (i.e. Cure) and other computer graphics applications.

Summary of key ClipperLib2 Features Relevant to AM and their use in PySLM

  • Improved performance and numerical robustness
  • Simplification of open-path clipping – no requirement to use PolyPath usage
  • Built-in numerical scaling between floating point and the internal Int64
  • Additional point attributes built-in directly (Z-attribute)

Summary of Implementation

The structure follows closely with ClipperLib2 api in most cases but has adapted some of the naming to be more pythonic and regularity during typing.

The added benefit of the original PyClipper library is that it can take numpy and native python lists directly, because these are implicitly converted by pybind into the internal vector format. A significant addition is the ability to accept 2D paths with the additional ‘Z’ attributes (currently floating points) without using separate functions, taking advantage of pythons duck typing. Open-paths and these optionally defined z attributes are returned when passing the arguments when performing the execute function for clipping utilities. Below are a summary of the key operations

Path Offsetting

Path offsetting is accomplished relatively straightforwardly. Paths are added to the ClipperOffset object and the join and end types are set. The delta or offset distance is then provided in the execute function. 

import numpy as np
import pyclipr

# Tuple definition of a path
path = [(0.0, 0.), (0, 105.1234), (100, 105.1234), (100, 0), (0, 0)]
path2 = [(0, 0), (0, 50), (100, 50), (100, 0), (0,0)]

# Create an offsetting object
po = pyclipr.ClipperOffset()

# Set the scale factor to convert to internal integer representation
pc.scaleFactor = int(1000)

# add the path - ensuring to use Polygon for the endType argument
po.addPath(np.array(path), pyclipr.Miter, pyclipr.Polygon)

# Apply the offsetting operation using a delta.
offsetSquare = po.execute(10.0)

Polygon Intersection

Polygon intersection can be perform by using the Clipper object. This requires add individual path or paths and then setting these as subject and clip. The execute call is used and can return multiple outputs depending on the clipping operation. This includes open-paths or Z attribute information.

# continued 

# Create a clipping object
pc = pyclipr.Clipper()
pc.scaleFactor = int(1000) # Scale factor is the precision offered by the native Clipperlib2 libraries

# Add the paths to the clipping object. Ensure the subject and clip arguments are set to differentiate
# the paths during the Boolean operation. The final argument specifies if the path is
# open.

pc.addPaths(offsetSquare, pyclipr.Subject)
pc.addPath(np.array(path2), pyclipr.Clip)

""" Polygon Clipping """
# Below returns paths of various clipping modes
outIntersect  = pc.execute(pyclipr.Intersection)
outUnion = pc.execute(pyclipr.Union)
outDifference = pc.execute(pyclipr.Difference, pyclipr.EvenOdd) # Polygon ordering can be set in the final argument
outXor = pc.execute(pyclipr.Xor, pyclipr.EvenOdd)

# Using execute2 returns a PolyTree structure that provides hierarchical information
# if the paths are interior or exterior

outPoly = pc.execute2(pyclipr.Intersection, pyclipr.EvenOdd)

Open Path Clipping

Open-path clipping (e.g. line segments) may be performed natively within pyclipr, by default this is disabled. Within the execute function, returnOpenPaths argument should be set true. 


""" Open Path Clipping """
# Pyclipr can be used for clipping open paths.  This remains simple to complete using the Clipper2 library

pc = pyclipr.Clipper()
pc2.scaleFactor = int(1e5)

# The open path is added as a subject (note the final argument is set to True to indicate Open Path)
pc2.addPath( ((50,-10),(50,110)), pyclipr.Subject, True)

# The clipping object is usually set to the Polygon
pc2.addPaths(offsetSquare, pyclipr.Clip, False)

""" Test the return types for open path clipping with option enabled"""
# The returnOpenPaths argument is set to True to return the open paths. Note this function only works
# well using the Boolean intersection option

outC = pc2.execute(pyclipr.Intersection, pyclipr.NonZero)
outC2, openPathsC = pc2.execute(pyclipr.Intersection, pyclipr.NonZero, returnOpenPaths=True)

Z-Attributes

The final script of note is the in-built Z attributes that are embedded within PyClipr. Z attributes (float64) can be attached to each point across a path or. set of polygons. During intersection of segments or edges, these Z attributes are passed to the resultant clipped paths. These are returned as a separate list in the output.

""" Test Open Path Clipping """

pc3 = pyclipr.Clipper()
pc3.scaleFactor = int(1e6)

pc3.addPath(openPathPolyClipper, pyclipr.Clip, False)

# Add the hatch lines (note these are open-paths)
pc3.addPath( ((50.0,-20, 3.0),
              (50.0 ,150,3.0)), pyclipr.Subject, True) # Open path with z-attribute of 3 at each path point

""" Test the return types for open path clipping with different options selected """
hatchClip = pc3.execute(pyclipr.Intersection, pyclipr.EvenOdd, returnOpenPaths=True)

# Clip but return with the associated z-attributes
hatchClipWithZ = pc3.execute(pyclipr.Intersection, pyclipr.EvenOdd, returnOpenPaths=True, returnZ=True)

Usage in PySLM

PyClipr has been refactored for use in the next release of PySLM (v0.6). This has improved readability of code and in some cases there are performance improvements due to inherent optimisations within ClipperLib2. This includes also removal of unnecessary transformations and scaling factors performed within python, that were required converting between paths generated in PySLM (shapely) and PyClipper originally. In particular, avoiding the use of PolyNodes were especially useful to avoid throughout. Modifications have been applied throughout the entire modules including the hatching and support modules. PySLM also now benefits by becoming a purely a source distribution, by distribution the clipping and offsetting functions into a separate package, therefore no additional compiling is required during installation.

Export L-PBF Scan Vectors to VTK/Paraview via PySLM

3D Printing Additive Manufacturing Blog L-PBF PySLM No Comments

The in-built visualisation for scan paths in PySLM leverages matplotlib – refer to a previous post. This is sufficient for most user’s needs when attempting to interpret and visualise the scan paths generated in PySLM, or those imported from a slice taken from an existing machine build files. Extending this beyond multiple layers or large parts becomes more tricky when factoring in visualisation of some parameters (e.g. Laser Power, effective scan speed). Admittedly, the performance of Matplotlib becomes limited to explore the intricacies and complexities embedded within the scan vectors. 

For scientific research, the fusion of scan vector geometry with volumetric datasets such as X-Ray CT during post-inspection of parts/samples, or those generated within the build process including pyrometry data, thermal-imaging offer the ability to increase our understanding and insight to observations of the effect of process on the material produced using L-PBF.  GPU based visualisation libraries such (vispy) would offer the possibility to accelerate the performance, but are not user-friendly nor offer interactivity when manipulating views and the data and are often cumbersome when processing volumetric datasets often encountered in Additive Manufacturing. Paraview is a cross-platform open-source scientific visualisation tool that is especially powerful for processing, interaction and visualisation of large-scale scientific datasets.

Paraview and the underlying VTK library offers an alternative ready-made solution to visualise this information, and are most importantly hardware accelerated with the option for raytracing provided by OSPRay and OptiX for latest RTX NVIDIA cards that include Raytracing (RT) cores. Additionally, the data can be augmented and processed using parallelised filters and tools in Paraview.

VTK File Format

Ignoring the HDF5 variations that are most useful for structured data, the underlying format within vtk that used for storing vector based data and point cloud data is the .vtp file format. The modern VTK file formats use an XML schema – unlike the legacy format, to store a structured series of geometry (volumetric data, lines, polygons, 3D elements and point clouds). The internal data format can be stored using ascii encoding or binary. Binary data can be incorporated directly within a parsable .xml format using a Base64 encoding and may additional incorporate internal compression. Alternatively data can be stored in an appended data section located at the footer of the file, which treats data section as a contiguous block of raw data. Different sub-formats exist, that are appropriate for different types of data e.g. volumetric, element based (Finite Volume / Finite Element derived) or polygon based. An approach relevant to export scan vector geometry the .vtp – format is most suitable.

The data stored in the VTK Point file consists of:

  • 3D points coordinates
  • Data attributes stored at each point location
  • Geometric elements (lines, polygons) defining connectivity with reference to the list of point coordinates

Paraview exporter implementation:

The Paraview exporter is simplistic, because the data compression is currently ignored. The process is similar to the technique used in the function pyslm.visualise.plotSequential, whereby hatch and contour vectors are merged and reprocessed in order that they represent always a series of lines (an n x 2 x 2 array). This is not the most efficient option for ContourGeometry (border scans) where scan vectors are continuously joined up, but simplifies the processing working with the data.  

Once the scan vector coordinates and the relevant data are packaged up into a single array, the data is wrote within the sub-sections of the XML file. Data is stored using floating points or integers accordingly in a binary representation. The data used to represent coordinates and indices for each vector, are stored with the ‘appended’ option within the <DataArray> element of each section. The raw data is stored and collected that are then written in the <AppendedData> element at the end of file with raw encoding option chosen. The byte offsets for the position of each ‘chunk’ of data that are referenced by the <DataArray> element are collected and stored incrementally.

For reference, the following information is provided for writing raw data, because this was difficult to obtain from the VTK documentation directly.

<AppendedData encoding=”raw”> Start of Raw Data Section
_ Underscore character is starting location for reading raw data
Section Size (Int32/Int64)Integer representing size of following section (include the size in bytes
with the offsets provided). The integer type should match the size used in the header.
Raw data (e.g Int32, float32, float64)
….Repeated the above (two rows) for each referenced data section
</AppendedData>

Example Scan Vector Data exported to VTK

An example Aconity .ILT file was imported into PySLM and then exported to a .vtp VTK file that was processed in Paraview. The scan order is visualised by the colour map with each vertex assigned a global-id. The ‘Tube‘ filter was applied to each scan vector in order to improve their visibility.

Visualisation scan-vectors for L-PBF/SLM processed in PySLM and exported to VTK (.vtp) file format

The script excerpt can currently be found on a Gist. This will be later included in future versions of PySLM along with other import/exporters.

GPU 3D Printing Slicer for DLP/Jetting using PySLM

3D Printing Additive Manufacturing Blog PySLM No Comments
Anycubic Digital Light Projection (DLP) 3D Printer System used for Slicing
Anycubic DLP 3D Printer System

Digital Light Projector (DLP) 3D Printers are an exceptionally productive technique for producing highly detailed (30<𝝁m) parts at high speeds at minimal costs.The CLIP process is a further enhancement in build speeds.

Briefly, the DLP process is similar to Stereolithography (SLA). It cures a vat of UV curable polymer material above a flexible transparent PTFE membrane. Instead of a single exposure (UV laser) into the resin, a monochrome LCD screen is used to mask the UV exposure source underneath. A greyscale bitmap image is used for each layer. Typically for most systems, after exposing the layer (1.5-3 s), the upper build-platform retracts, and mechanically pulls the cured layer away from the flexible membrane and the process is repeated. Surprisingly simple, but effective in cost and the production speed.

Additionally, bitmap based approaches are used amongst Material Jetting (MJ) technologies predominantly used within our research group CfAM, at Nottingham. Both DLP and Material Jetting offer high resolution between 30-100 𝝁m both in the XY slice plane dependent on the printer, and for Inkjet downwards of 1-10 𝝁m layer thickness depending on the choice of ink loading. Accordingly, these high resolutions are demanding to print. I came accustomed to using these printers in our CfAM lab at Nottingham on a recent project. The affordability of these printers is genuinely remarkable, owing to their mechanical simplicity.

Based on a previous post back in 2016 by Dr Matt Keeter, this is an excellent reference to an approach using WebGL implementation. Their post introduced the method, but the approach was obscured by its WebGL based implementation. Frutstratingly, I never came across an implementation for use in a research environment. These appraoches are most likely used in the free slicer software provided for desktop DLP 3D Printers.

DLP 3D Printer - Anycubic Mono 4k - Nottingham Lab
Anycubic Mono 4k DLP Printer at the University of Nottingham’s CfAM Lab loaded with a composite ink. 2022.

Interestingly, this approach can also be extended for generating 3D voxel models, by applying the project across multiple directions. However, the reliability of such method for non-manifold meshes would likely be limiting.

Method for Bitmap Slicing

The method is similar and use the same infrastructure to that used in the previous post for performing height map ray projection. Likewise, to provide a cross-platform compatibility, the use of Vispy and OpenGL 2.0 GLSL shaders are utilised within a single script. As such, the resolution of the output is limited to the maximum framebuffer size supported by the GPU driver on the system.

The approach for generating slices relies on having a connected watertight with surface triangles normals correctly orientated (fixable natively using Trimesh). The approach uses a combination of Stencil buffers integrated natively in GPU hardware.

By choosing an appropriate Z-clipping plane for the camera, the Stencil buffer is used to keep and discard rasterised triangles with the z-clipping range based on the Z-order. In order to determine if the fragments rendered are inside or outside the mesh. The render pipeline uses three passes:

  • Pass 1: stencil buffer increments on front facing fragments
  • Pass 2: stencil buffer decrements on back facing fragments
  • Pass 3: discard fragments where the stencil buffer is zero

During all the render passes, GL Depth tests are turned off. Typically in 3D Programs, triangles that are obscured from view of the 3D camera, or hidden behind other triangles are culled and the fragment is discarded prior to rendering . In this method, depth testing is turned off. The full approach is detailed further in the excerpt below inside the on_draw call.

def on_draw(self, event):

    with self._fbo:
        # Set the GL state
        gloo.set_state(blend=False, stencil_test=True, depth_test=False, polygon_offset_fill=False, cull_face=False)

        # Set the size of the framebuffer to fit the geometry with the correct aspect ratio
        gloo.set_viewport(0, 0, self._visSize[0], self._visSize[1])
        gloo.set_clear_stencil(0)
        gloo.set_clear_color((0.0, 0.0, 0.0, 0.0))
        
        # Clear the framebuffer
        gloo.clear()

        self.program['bounds'] = self.bbox[0,2], self.bbox[1,2]
        self.program['aspect'] = self.physical_size[1] /  self.physical_size[0]
        
        # The position of the slice position passed to the GLSL shader
        self.program['frac'] = self._z * 2.0 

        # Draw twice, adding and subtracting values in the stencil buffer

        # Render Pass 1 (Increment Stencil Buffers)
        gloo.set_stencil_func('always', 0, 0xff)
        gloo.set_stencil_op('keep', 'keep', 'incr', 'back')
        gloo.set_stencil_op('keep', 'keep', 'keep', 'front')
        self.program.draw('triangles', self.filled_buf)

        # Render Pass 2 (Decrease Stencil Buffers)
        gloo.set_stencil_op('keep', 'keep', 'decr', 'front')
        gloo.set_stencil_op('keep', 'keep', 'keep', 'back')
        self.program.draw('triangles', self.filled_buf)

        # Clear only the color buffer
        gloo.clear(color=True, depth=False, stencil=False)

        # Render Pass 3
        gloo.set_stencil_func('notequal', 0, 0xff)
        gloo.set_stencil_op('keep', 'keep', 'keep')
        self.program.draw('triangles', self.filled_buf)

        # Store the final framebuffer 
        self.rgb = _screenshot((0, 0, self._visSize[0], self._visSize[1]))

The GLSL shaders are not particularly interesting. Focus should be given to the Vertex shader, rather than the Fragment shader. This Vertex shader processes vertices of the mesh and applies the Model View Projection (MVP) transformation matrix onto the input mesh. The MVP matrix is chosen to scale the entire geometry so that it fits within the Z-clipping range of Z = -1 to +1, and is within the scope of rendering into Stencil buffer whilst using the 3D Orthographic Camera. Finally, the model is transformed based on a fractional range (0-1) to obtain the required Z-slicing plane. An epsilon value is provided for round-off purposes. 

uniform   mat4 u_model; // Model transform matrix
uniform   mat4 u_view;
uniform   mat4 u_projection;

uniform  vec2 bounds; // Z bounds
uniform  float frac;  // Z fraction (0 to 1)
uniform  float aspect; // Aspect ratio

attribute vec3 a_position;

#define EPSILON 0.001

void main() {

    vec3 pos = a_position;
    
    // Ensure the bottom of the part is positioned to z=0 using the bottom bounding box
    pos.z -= bounds[0];
    
    // Scale the so that it fits within the clipping range (-1.0 < z < 1.0)
    pos.z *= -2.0/(bounds[1]-bounds[0]);
    
    // Adjust the position of  the verticies 
    pos.z -= frac;  
    gl_Position = u_projection * u_view * u_model * vec4(pos, 1.0);
    gl_Position.z += 1.0 - EPSILON;
}

The remainder of the script sets up the infrastructure for Vispy. This is performed within the initialisation call for the script. This methods sets up the correct OpenGL state, viewport size including the use of an off-screen render and specific selection of a separate Stencil framebuffer used to render onto. Both the vertex and fragment shaders are compiled and the transformation matrix is generated based on an Orthographic projection sized to the bounding box of the geometry.


    # Window Size
    shape = int(self._visSize[1]), int(self._visSize[0])

    # Create the render texture used by default in the pipeline
    self._rendertex = gloo.Texture2D((shape + (4,)), format='rgba', internalformat='rgba32f')
    
    # These are not used but are for reference
    #self._colorBuffer = gloo.RenderBuffer(self.shape, format='color')
    #self._depthRenderBuffer = gloo.RenderBuffer(shape, format='depth')

    # Create the stencil buffer (8 bit component)
    self._stencilRenderBuffer = gloo.RenderBuffer(shape, format='stencil')
    self._stencilRenderBuffer.resize(shape, format=gloo.gl.GL_STENCIL_INDEX8)

    # Create FBO, attach the color buffer and depth buffer
    self._fbo = gloo.FrameBuffer(self._rendertex)
    self._fbo.stencil_buffer=self._stencilRenderBuffer

    # Set the size of the view port based on the size of the window (the bounding box)
    gloo.set_viewport(0, 0, self.physical_size[0], self.physical_size[1])
    gloo.set_viewport(0, 0, self._visSize[0], self._visSize[1])

    # Create the initial orthographic view projection transformation based on the bounding box of the geometry
    self.projection = ortho(self.bbox[1, 0], self.bbox[0, 0], self.bbox[1, 1], self.bbox[0, 1], 2, 40)
    # Identity matrix
    self.model = np.eye(4, dtype=np.float32)

     # Set MVP variables for shaders
    self.program['u_projection'] = self.projection
    self.program['u_model'] = self.model
    self.program['u_view'] = self.view

Other operations are processing and the Trimesh and correctly transformed into the correct position:

The script was applied to a porous aerofoil structure with an XY resolution of 20 µm that was used previously on an Anycubic DLP system. Below is an example cross-section taken using this approach. Notice the high resolution

GPU 3D Printing Slicer used on an aerofoil structure

Conclusions

The overall approach may have a limited use by itself. Generally, the need to bespoke high resolution slices are limited at this stage. For reference, the full excerpt of the script is temporarily located here. In future, I will consider including this as another option within PySLM.

The source code can be found below or on GitHub:

PySLM 0.5

Additive Manufacturing Blog PySLM No Comments

PySLM 0.5 has had a long incarnation. It has been waiting in anticipation for the past year and delayed due to challenges with the coding and ensuring cross-compatibility. It is an exciting release and a testament to the relative maturity of the project. Already, it is fantastic to observe that it is providing a great positive contribution and benefit to the research in the Additive Manufacturing community. Once again, I wish to personally thank everyone’s support developing this along the way.

The highlight of the 0.5 release is the addition of the new Support Module. The Support Module provides the building-blocks and the infrastructure to identify and extract support volumes, and generate their support structures based on meshes provided as input. The module has been in development in the background for over two-three years and finally, reaching a level of maturity that was in a position to release into the public.

The tools include the usual and standard technique of extracting overhang surfaces, edges and points based on the on their facial connectivity which was discussed in a previous post. These surfaces are used as the input in a ray-tracing approach for identifying precise volumetric block support structures as shown above. Unlike most implementations available externally, these conform to the boundaries of the part, utilising a new boolean CSG library PyCork, which provides a cross-platform Python implementation of the Cork Library. Due to limitations in existing CSG approaches available, a fast GPU based ray-trace approach is utilised to project identified support surfaces and create a high-resolution projection height-map to locate self-intersections like below. Furthermore, these provide additional flexibility to create alternatives approaches, such as those suitable for other manufacturing processes e.g. point-support structures (e.g. in SLA) or tree like support structures.

GPU Generated Depth Projection Maps

Each support surface identifies self-intersections with the original part and those with the build platform. The regions are segmented using an image processing technique based on an overhang tolerance and transformed into polygon boundaries. Simplification is necessary and use a combination of the Douglas-Peucker algorithm within scikit image’s approximate_polygon function and b-spline fitting tool available in Scipy. The boundary simplification is useful to alleviate issues when encountering sharp features extracted from jagged edges in the support regions.

These volumetric regions provide the foundational elements for constructing sophisticated support structures, especially those used within SLM systems. To maximise productivity, provide greater control over controlling distortion due to residual stress, grid-truss based support structures have been utilised for over a decade in SLM. Unfortunately, I have yet an to come across a known implementation that exists both in literature nor open-source code to generate these structures. Below is an example of conformal grid-truss geometry generated for a complex topology optimised bracket component.

In the implementation, the grid truss structure is generated by taking cross-sections throughout the support volumes and using a geometric polygon operations offered by the ClipperLib. The truss is formed by generating hatch lines that are offset and union to create a truss. This approach provides flexibility to design different structures. Afterwards, 3D triangular meshes are generated from the polygon boundaries which are mapped back onto the original support volume. Doing this efficiently is challenging given the potential size and number of support structures that can be generated.

Under own testing, the implementation is reliable for most geometries, although there are few known cases where the algorithm will not work. It is acknowledged that the support module is not intended to be a direct replacement for commercial software, rather, provide a working reference that researchers and general users can understand, adapt and utilise in their own work/research or part of a pipeline.

An example script for generating a support structure can be found on the Github repository in examples/example_support_structure.py

The installation of PySLM 0.5 has soft-dependencies for using the support module due to the additional algorithms required. Please, ensure that these are all installed and that there is a working OpenGL 2.1 installation (via Vispy and PyQt5) on your system. The core functionality offered in PyQt5 may be utilised without these extra dependencies for those wanting a simplified installation.

Opportunities to explore:

There are many opportunities that are available to investigate using the new functionality available: e.g. lattice based support structures, alternative approaches support structures, novel scan strategies suitable for SLM. Parametric and optimisation of the support structure design – e.g. automated support generation. The tool will aid those working in modelling and simulation: optimisation of designs prior to printing to account for distortion, control of thermal history, globally optimise parts for build-cost-time models. It would be great to hear from anyone on their experience using this functionality.

Further improvements to PySLM

The remainder of the release has a few improvements and fixes to the core functionality and its documentation. It is important to highlight the analysis module for predicting build times – accounting for scan vector jump delays, jump speed, point exposure delays that have an incremental impact on the overall build time. Additionally, the release has been tested across all platforms (Windows, Linux, Mac OS X) and further testing and maturity of libSLM‘s translators continue: including a working implementation of EOS .sli format.

The full release log for PySLM 0.5 may be found in Changelog.MD

Overhang and Support Structures in L-PBF (SLM) using PySLM (Part I)

3D Printing Additive Manufacturing Blog L-PBF PySLM No Comments

A key focus of the release of PySLM 0.5 was the introduction of support structure generation targeted for powder-bed fusion (PBF) processes such as Selective Laser Melting (SLM) and also Electron Beam Melting (EBM). The basic infrastructure for generating support structures was developed including overhang analysis, support projection maps and the calculating precise conforming volumes, that leads to demonstration of block ‘truss’ based supports.

It is a particularly exciting release, because it is the first implementation both open source but also explicitly documents in practice a potential method for generating support structures for these specific PBF processes that have commercially (albeit few choices) been available for over a decade.

The challenge of this specific problem was to provide a robust solution covering the majority of engineering cases – which led to the length of time taken to develop this feature. This included having to develop many additional functions, support routines and workarounds for the limited availability of a boolean CSG library for triangular meshes in Python whilst providing reasonable performance.

In the Support Structure, the geometry constructed consists of a grid and a boundary which features a polygon derived truss structure in order to support powder removal and control the stiffness of the structure. Below highlights the capability for generated truss-based support structure suitable for PBF process. Carefully observe that individual support blocks are separated when self-intersecting and precisely conform to the original geometry. The support volumes themselves interface with the original part, by performing an exact boolean intersection.

Truss based Support Structures for Selective Laser Melting (SLM) or LPBF generated using PySLM
Support Structure Generation in PySLM 0.5 suitable for Selective Laser Melting. Separate support regions are generated for the part using a projection method and a truss based support structure is generated in a grid and along the boundary.

Within the support volumes generating a grid-truss support structure can be generated by taking 2D cross-sections and applying various polygon clipping techniques to generate the structure to create the truss. These trusses structure are particularly more efficient for scanning as these slice as individual scan vectors rather than a series of point exposure.

PySLM: Python 3D Printing support generation for selective laser melting - bottom view showing a grid truss support
A view from the bottom showing the grid truss support structure generated
PySLM: Slicing through a generated SLM Support Structure generated using PySLM.
A slice or cross-section taken through both the part and support structures. It can bee seen that the support structure is constructed from a grid which represented single linear scan vectors during scanning.

Future work intends to correctly hatch the support structure regions and integrate a multi-body slice and hatching procedure, but this is intended for inclusion in a future release, possibly PySLM 0.6.

Due to the implementation’s brevity, the proposed methodology will be split across multiple-posts. Anecdotally, work began on a support method over two years ago, intended to offer a more complete input towards deriving a cost model based on existing research in the literature – for further guidance refer to the following posts (Build time estimation).

Background on Support Structures

Support structures are a vital element to Additive Manufacturing. Despite the additional cost of post-processing support structures, these are useful and in some instances essential for successful manufacture of metal AM parts. Most 3D printed users will be very familiar with support generation: the tedious removal of additional structures in most AM processes (FDM, SLM, SLA, BJF, EBM) and the practical difficulty removing this material afterwards. SLS/HSS for polymer parts are largely immune from this manufacturing constraint and make it as a technology for every attractive and cost efficient to produce 3D printed parts without much specific knowledge from the designer. They serve a variety of purposes beyond geometrically supporting overhang surfaces, namely:

  • Anchor the part onto to the build platform before removal using Spark Erosion or Wire Electric Discharge Machining
  • Counter-act distortion in materials prone to residual stresses, when compensation factors cannot be used through AM build simulations
  • Provide a path to dissipate heat to prevent overheating of regions,
  • Provide structure to support forces exerted during post machining interfaces.

Even with the best intention for the engineer or technician to design these out, it is likely that these may need to be included. On-going development and research to adapt topology optimisation [1][2][3][4][5][6] to support ‘overhang constraints’ or specifically minimise boundaries with support angles that require support has progressed within recent years since the time of this post. Research has also considered using topology optimisation to structurally derive support structures based on an ‘inherent strain’ or distortion as an input [7]. Infact, are now available as design constraints within commercial Topology Optimisation software. However, momentarily these are currently not a complete or holistic solution. By their inclusion, there is a detriment to the overall performance of the solution optimsed. They also do not factor other objective functions such as minimising support material, overhang surfaces, part anisotropy and crucially the piece part cost [8][9]. In industrial applications, the part functionality or fundamental shape may make this challenging or penalise the algorithms. ‘Generative’ approaches, may globally optimise the part (including orientation) to minimise the requirements of support structures, but it is inevitable that some use is required. Geometrically, the quality or surface roughness of overhang or down-skin surfaces are improving through process optimisation of the laser parameters provide by the OEMs. There are indications that the choice of powder size and the layer thickness may improve the surface finish of these problematic regions.

Under some situations support structures can minimise the risk taken to manufacture parts first-time and ultimately reduce the cost of a supplier delivering the part to the customer. It also provides paths to dissipate excess heat generated which will become a further challenge to overcome with the adoption of multiple-laser SLM systems. Research has also proposed different support structures strategies for mitigating the effects of overheating and distortion in the SLM process [10], which included using topology optimisation to find thermally efficient support structures for heat transfer.

Support Structure Generation Capability in existing AM Pre-processing Software

For the specific area of interest for PySLM, it is a particular challenging requirement that remains to be overcome in selective laser melting and to a much lesser extent electron beam melting. The generation of support structures in FDM and SLA technologies is well established and available in consumer-led software for popular FDM printers such as Ultimaker Cura, Slic3r, SLA Formula’s Preform for SLA, or Chitubox for DLP . Fortunately, some of these software are opensource and provide some reference to how these are generated and successfully adopted across FDM 3D printing. Arguably, I have yet to delve into methods for how these are generated but it is expected the supports generated are similar to that used in metal AM . In metal additive manufacturing, commercial capability is available in both Materialise’s Magics SG/SG+ Module, Netfabb and to some existing OEM software. A reference and implementation of support generation for commercial or industrial led 3D printing especially in metal additive manufacturing is currently non-existent. These software are known to be relatively expensive to purchase and maintain.

Support Structure Generation in Research

In academic literature, the use of commerical software for support generation covers a couple of common research areas in the AM Literature including:

  • Part assessment: part buildability, overhang analysis
  • Process planning and optimisation: build-time prediction, build volume packing, cost modelling
  • Distortion and support minimisation: Numerical simulation to minimise distortion and support structure requirements
  • Lattice structures: minimising support structure requirements

Further overview of current work and research in Support Structures is also reported [11]. Specifically concerning about support generation in Laser PBF processes for these posts, support generation remains an outstanding challenge with the process.

Overhang Areas

Overhang areas are characterised as those prone to generate surfaces that do not conform to the intended geometry of the digital model. These usually result in with surfaces of high roughness / poor surface quality or formation of ‘dross’. These underlying regions may be susceptible to defect inclusions due to the localised overheating, due to the insulative behaviour of powder underneath the exposure zone. Fundamentally, Overhang areas correspond with the build-up of geometry inclined at shallow angles inclined against the build direction i.e. ‘overhang-angle’. It is dependent on many factors including the

  • machine system,
  • material alloy processed,
  • layer thickness,
  • optimisation of laser parameters (the down-skin parameter set).

Completely unsupported areas – those which do not have any solid material underneath, exasperate this effect. Under some situations, the support material become disconnected and dislodged by the powder spreading or re-coating mechanism, which in the extreme case may cause build-failure.

Mitigating the Effects of Distortion due to Residual stress

Some metal alloys are susceptible to the effects of residual stress generation, in particular Titanium. These stresses manifest with the manufactured part due to thermal-gradients. The effect of residual stress is that it generates internal forces causing distortion of the part. In the extreme situations, it can cause failure due of material due to stresses exceeding the material yield-point. During the build-process, it causes parts to ‘curl’ upwards. This can be somewhat mitigated to an extent using strong enough support structures in the correct place. It can be decided through the intuition the of the machine operator or now through the use of dedicated AM build simulation software. Various research has investigated the optimisation of support structures based on distortion of parts [12].

Much further could be discussed about the area of residual stress in detail but it can be further looked at within the literature. A future post may focus on this in greater detail.

Challenges Created by Support Structures

Amongst post-finishing requirements to achieve required tolerances of a manufactured part it contributes a significant cost to the end-part when they cannot be avoided.

Removal of metal supports is unpleasant and unsatisfactory stage of the manufacturing process. This is dependent on the hardness/strength of the material alloy and the type of supports utilised. They open up the myriad of variability from ‘hand-fettled‘ or ‘artisan’ finishes achieved through support – often referred as the artisanal craft of 3D printing. Even post machining the supports of is an additional process, that requires setup and also the time to prepare the part on the CNC machine. Perhaps, the utilisation of robotic CNC machining in the future will significantly reduce the cost of support removal as part of serial production. It would be fantastic to see some exploration integrating CNC machining of support removal directly from PySLM and is a move towards digital twins.

Support structure contribute the following (in)-direct intrinsic costs for a part produced by metal AM:

  • Indirect impact on functional performance by designing around overhang constraints
  • The additional time and cost for the designer to correctly generate the support – including simulation time
  • The direct cost of building the support structures on the system
  • The support removal time (machined or hand removed)
  • Direct impact on the e.g. total performance of the part due to this constraint e.g. surface roughness impacting fluid flow, fatigue performance

Aims of the PySLM Support Module for Support Structures

Support generation capability in PySLM aims to provide a working reference for other researchers to adopt amongst their work. Thus assist researcher’s understand and explore the generation of various types of common support structures employed in AM. Also, it will enable the entire AM ecosystem to have some capability that it can be adapted accordingly for their own wishes.

It does not intend to guarantee to provide a production ready support generation for metal AM parts without careful attention. In the future, this will expand to explore various approaches and further refine capability for PySLM to be a more comprehensive toolbox for use in AM research.

See the Next Post in the Support Structure Series

References

References
↑1 Serphos, M. R. (2014). Incorporating AM-specific Manufacturing Constraints into Topology Optimization. Delft University of Technology.
↑2 Leary, M., Merli, L., Torti, F., Mazur, M., & Brandt, M. (2014). Optimal Topology for Additive Manufacture: A method for enabling additive manufacture of support-free optimal structures. Materials & Design, 63, 678–690. https://doi.org/10.1016/j.matdes.2014.06.015
↑3 Gaynor, A. T., & Guest, J. K. (2016). Topology optimization considering overhang constraints: Eliminating sacrificial support material in additive manufacturing through design. Structural and Multidisciplinary Optimization, 54(5), 1157–1172. https://doi.org/10.1007/s00158-016-1551-x
↑4 Garaigordobil, A., Ansola, R., Santamaría, J., & Fernández de Bustos, I. (2018). A new overhang constraint for topology optimization of self-supporting structures in additive manufacturing. Structural and Multidisciplinary Optimization, 58(5), 2003–2017. https://doi.org/10.1007/s00158-018-2010-7
↑5 Gaynor, A. T. (2015). Topology Optimization Algorithms for Additive Manufacturing. Retrieved from https://jscholarship.library.jhu.edu/bitstream/handle/1774.2/38009/GAYNOR-DISSERTATION-2015.pdf
↑6 Allaire, G., Bihr, M., & Bogosel, B. (2020). Support optimization in additive manufacturing for geometric and thermo-mechanical constraints. Structural and Multidisciplinary Optimization, 61(6), 2377–2399. https://doi.org/10.1007/s00158-020-02551-1
↑7 Zhang, Z. D., Ibhadode, O., Ali, U., Dibia, C. F., Rahnama, P., Bonakdar, A., & Toyserkani, E. (2020). Topology optimization parallel-computing framework based on the inherent strain method for support structure design in laser powder-bed fusion additive manufacturing. International Journal of Mechanics and Materials in Design, 0123456789. https://doi.org/10.1007/s10999-020-09494-x
↑8 Brackett, D., Ashcroft, I., & Hague, R. (2011). Topology optimization for additive manufacturing. Solid Freeform Fabrication Symposium, 348–362. Retrieved from http://utwired.engr.utexas.edu/lff/symposium/proceedingsarchive/pubs/Manuscripts/2011/2011-27-Brackett.pdf
↑9 Brika, S. E., Mezzetta, J., Brochu, M., & Zhao, Y. F. (2017). Multi-Objective Build Orientation Optimization for Powder Bed Fusion by Laser. Volume 2: Additive Manufacturing; Materials, (August), V002T01A010. https://doi.org/10.1115/MSEC2017-2796
↑10 Paggi, U., Ranjan, R., Thijs, L., Ayas, C., Langelaar, M., van Keulen, F., & van Hooreweder, B. (2019). New support structures for reduced overheating on downfacing regions of direct metal printed parts. Solid Freeform Fabrication 2019: Proceedings of the 30th Annual International Solid Freeform Fabrication Symposium – An Additive Manufacturing Conference, SFF 2019, 1626–1640. Austin, Texas, USA.
↑11 Jiang, J., Xu, X., & Stringer, J. (2018). Support Structures for Additive Manufacturing: A Review. Journal of Manufacturing and Materials Processing, 2(4), 64. https://doi.org/10.3390/jmmp2040064
↑12 Krol, T. A., Zaeh, M. F., Seidel, C., & Muenchen, T. U. (2012). Optimization of supports in metal-based additive manufacturing by means of finite element models. SFF, 707–718.

PySLM: Geometric Hatch Overlap Check/Visualisation

Additive Manufacturing Blog PySLM No Comments

Designing scan strategies for PBF techniques, we are not entirely aware of situations that arise where the powder-bed is not fully exposed due to a mismatch when scan vectors are not sufficiently overlapped. Typically, unoptimised placement of hatch vectors lead to the creation of irregular porosity or voids in L-PBF parts.

This can arise along the intersections between the contour and interior hatches, especially a long concave regions such as sharp corner features with acute angles.

The approach is not an efficient way to examine the presence of , but provides a representative view for checking this geometrically.

Method

The approach takes advantage of the relatively new Iterator classes available within the analysis module, which vastly simplifies the generation procedure for manipulating and examining existing scan vector geometry. Firstly, generate or alternatively import the Layer and its LayerGeometry groups to examine. The group of layers are passed to the ScanVectorIterator class, which will iterate across every scan vector from both ContourGeometry and HatchGeometry objects within a Layer. Single point exposures are not considered. 

import pyslm.analysis
from shapely.geometry import LineString, Polygon, MultiPolygon
from shapely.ops import cascaded_union

scanIterator =  pyslm.analysis.ScanVectorIterator([layer])

After the creation of the ScanVectorIterator, this can be readily expedited to process across all scan vectors across the Layer. The basic process relies on converting each scan vector to a Shapely polygon objects and then processing them using the geometry tools available.

For this case we use Pythonic notation to compactly operate across each scan vector and collect them. We convert each scan vector to a Shapely LineString, which has a method to then offset or buffer. 

# Laser Spot Radius
laserSpotRadius = 0.04

# Iterate across each scan vector and buffer than geometry
lines = [LineString(line).buffer(laserSpotRadius) for line in scanIterator]

After offseting all the lines, this can be easily visualised by conversion to a Shapely MultiPolygon. 

# Merged the offset lines into a Shapely Multi-Polygon Collection
multiPoly = MultiPolygon(lines)
pyslm.visualise.plotPolygon(multiPoly)

The geometrical result is shown below. It is relatively quick to generate and plot individual scan vectors as shown below:

Geometrical overlap of scan vectors in SLM processed by PySLM
Overlap of hatch vectors represented by geometrically offsetting the individual scan vectors within a Layer.

Each scan vector that is offset is represented by a Shapely.Polygon. It is trivial to perform a boolean operation with the Shapely library. Although, it is recommended to use the more efficient, albeit still relatively slow, shapely.ops.cascaded_union function to merge multiple geometries together:

# Cascaded union is a more efficient boolean merge for multiple polygon entities
multiPolyMerged = cascaded_union(multiPoly)

pyslm.visualise.plotPolygon(multiPolyMerged)

The combined result is shown here with a slightly smaller hatch distance to exaggerate the effect and highlight regions where the laser beam may not sufficiently provide exposure to the powder bed:

Illustration of regions that may
Regions that have insufficient coverage observed after performing a boolean merge after the scan vectors have been offset

This post shares a relatively simple example exploration using geometrical operations and the iterator class to understand potential issues related to hatch overlaps.

Final Conclusions

Potentially, this check could be extended into 3D using morphological operations. This would provide a more qualitative examination of porosity generation as a result of Furthermore, the combined use of Neural Networks or reduce order models could provide a representative exposure area to provide the geometrical offset in 2D and provide a prediction for coverage spatially in 3D.

PySLM Scan Path Iterator

Additive Manufacturing Blog PySLM No Comments

Historical Background

An upcoming key feature in PySLM is the Iterators primarily useful for simulation studies, such as predicting thermo-mechanical behavior of scan strategies. Much of this builds upon ideas in former work that was done during my PhD for investigating the generation of residual stress in selective laser melting. In that study, MSC Marc, a commercial Finite Element analysis package was used to predict residual stresses generated during the process. The discretised position and laser parameters of the exposure from the laser was controlled by combination of Fortran User Subroutines and libSLM, the former c++ library.

Prior to running, a configuration file was passed to the simulation, specifying the SLM machine build file used for simulating the scan paths. libSLM parsed the compatible build-file and then based on the current time and increment would interpolate the position of the exposure point and laser parameters during firing. Beyond this main functionality, there were additional house keeping required for running the simulation, including passing information between the programs, and also additional tools to efficiently seek at an arbitrarily point in time, the state and position of the laser. This was necessary for restarting simulations on a HPC and for adaptive time-stepping required to keep numerical stability. For efficient seeking across the layers and each layer geometry structure was cached within a tree, that could be parsed on demand if necessary. Much of the infrastructure was excessive, although the implementation had to be written in c++ or Fortran to be used by integrated with the commercial solver.

Although it is difficult to perceive the full benefit of having a Python version of the same functionality, there are some instances and some analysis codes where this could be of benefit for modelling this and other processes as well.

Implementation of PySLM Iterators

The implementation builds upon the existing design from the original libSLM library. For all the Iterator classes, similar to most of the other pyslm.analysis module’s tools, the list of Layers and Models with the Laser Parameters should be passed:

# Iterates across layer geometries
layerGeomIter = Iterator(models, layerList) 

# Iterates across individual scan vectors - currently only ContourGeometry/HatchGeometry
scanVectorIter = ScanVectorIterator(models, layerList) 

# Generates an scan exposure point iterator
scanIter = ScanIterator(models, layerList)

The first stage is building a time cache tree across each LayerGeometry. In practice, the cache tree structure is not necessary if the scan iterator iteratively increments along in time. Having a cache structure enables non-linear movement of the iterator across the entire build . It also provides a fast random-access lookup to seek to a specific Layer or LayerGeometry for use in simulations or analyses.

This structure is formed by iteratively measuring the total time taken to scan an individual LayerGeometry group which is stored in a tree node (TimeNode). The cumulative time taken to scan across each LayerGeometry TimeNode to provide the total scan time across the Layer. The TimeNode can be assigned child and parent nodes using the attributes (TimeNode.parent and TimeNode.children) in order to navigate across the entire tree. Each TimeNode provides a key-value pair (id, value) to store the reference LayerGeometry or Layer for simplified access.

The Cache Tree is generated and stored in the Base Class, Iterator and is generated in the private method (Iterator._generateCache) and stored in the attribute Iterator.tree. 

def _generateCache(self) -> None:
 self._tree = TimeNode() for layerId, layer in enumerate(self.layers):     # Create the layer     layerNode = TimeNode(self._tree, id=layerId, value=layer)     self._tree.children.append(layerNode)     for layerGeomId, layerGeom in enumerate(layer.geometry):         geomNode = TimeNode(layerNode, id=layerGeomId, value=layerGeom)         geomNode.time = getLayerGeometryTime(layerGeom, self._models)         layerNode.children.append(geomNode) self._cacheValid = True

The Iterator class has many useful facilities, such as build-time estimation, seeking access to the Layer or LayerGeometry at an arbitrary point in time. The class stores additional info such as the layer dwellTime – this can be re-implemented in a derived class. For implementing the iterator behavior used across all dependent classes it also stores the current time and reference pointers to the current Layer and LayerGeometry. Essentially the Iterator class can be used to iterate across each LayerGeometry within a build as a foundation to the other class. Each of these Iterator classes builds upon the magic methods available in Python: __iter__ and __next__ . The __iter__ method simply sets up the object and re-initialises the Iterators attributes. Once the cache tree is generated internally, it offers no penalty to generate a new iterator . Below is an excerpt taken from the ScanVectorIterator:

def __iter__(self):
    self._time = 0.0
    self._layerGeomTime = 0.0
    self._layerInc = 0
    self._layerGeomInc = 0

    return self

def __next__(self):
     if self._layerScanVecIt < len( self._layerScanVectors):
         scanVector = self._layerScanVectors[self._layerScanVecIt]
         self._layerScanVecIt += 1
         return scanVector
     else:
         # New layer
         if self._layerIt < len(self._layers):
             layerVectors = self.getLayerVectors(self._layers[self._layerIt])
             self._layerScanVectors = self.reshapeVectors(layerVectors)
             self._layerScanVecIt = 0
             self._layerIt += 1
             return self.next()
         else:
             raise StopIteration

The Iterator class and ScanVectorIterator class do not require much further attention, as the pointer to the geometry is incremented only. The ScanIterator class, however, is more useful for simulation and will be discussed further.

Scan Iterator Class

The ScanIterator class is used for incrementally advancing the exposure source across each scan vector. This is particularly important for visualising or simulating the AM process. The time increment is based on a chosen but adjustable timestep, and the laser parameters across each scan vector (i.e. the effective scan velocity) obtained from the assigned BuildStyle.

The exposure point is linearly interpolated across each scan vector based on the current time within the LayerGeometry depending on the type. For identifying the position, the cumulative distance is captured and the current timeOffset for the layer geometry is used to estimate the distance covered by the exposure source across the entire LayerGeometry section. For simplicity this assumes no acceleration terms and uses a constant velocity profile. Based on the timeOffset, the scan vector is obtained and then the final position is interpolated across the scan vector. 

laserVelocity = getEffectiveLaserSpeed(buildStyle)

# Find the cumulative distance across the scan vectors in the LayerGeometry (Contour)
delta = np.diff(layerGeom.coords, axis=0)
dist = np.hypot(delta[:,0], delta[:,1])
cumDist = np.cumsum(dist)
cumDist2 = np.insert(cumDist, 0,0)

# If the offsetDist calculated is outside of the cumulative distance then some error has occured
if offsetDist > cumDist2[-1]:
    raise Exception('Error offset distance > cumDist {:.3f}, {:.3f}'.format(offsetDist, cumDist2[-1]))

id = 0

# Find the id of the current scan vector given the time offset
for i, vec in enumerate(cumDist2):
    if offsetDist < vec:
        id = i
        break

# interpolate the position based on offset distance in the scan vector
linearOffset = (offsetDist - cumDist2[id-1]) / dist[id-1]
point = layerGeom.coords[id-1] + delta[id-1] * linearOffset

The above example is specifically for the contour geometry. Note the for loop is not particularly efficient but serves its purpose for identifying the Iterator’s current scan vector.

Iterator Use:

Each iterator can be subsequently called after using the iter method in a variety of pythonic ways:

#Create a scan vector iterator
ScanVectorIterator(models, layerList)

# Create a python iter object from a ScanVectorIterator
scanIter = iter(scanVectorIter)

# Get a single scan vector
firstScanVec = more(scanIter)

# Collect all the remaining scan vectors
scanVectors = np.array([point for point in scanIter])

Current Limitations:

Note the current implementation of the iterators currently only consider ContourGeometry and HatchGeometry and does not include PointGeometry groups. The jump vectors are ignored, which will have a small but in most situations a negligible effect on the the overall accuracy of the timing used for the iterators.

Another obvious limitation is that this only accounts for single exposure source systems. It is not known to myself, how multiple-exposure systems scan (i.e. are they truly in parallel based on the laser number) or is there is some built-in machine heuristic which balances the scanning across all laser sources and spatially – e.g. to prevent overheating. This depends on the SLM system such as if multiple exposure sources are limited by zones or have full areal access to the bed. Anyone’s comments or experiences on this aspect would be sincerely welcomed.

Example

An example showing the basic usage and functions available with the Iterator classes are available in the Github Repo examples/example_laser_iterator.py

PySLM Version 0.3

Additive Manufacturing Blog PySLM 3 Comments

PySLM version 0.3 was released last week to coincide with a large number requests from users of the library. The release is consists of many updates, fixes and examples accumulated across the last 6 months since last summer. Additional work was done to refine the release of the sister library libSLM and resolve some bugs that couldn’t be determined until exporting the machine files and testing on the machine, with acknowledgement of support from researchers who have got in touch. Many thanks for their assistance on this development journey.

The release notes can be found on github.

The original release was scheduled to include support generation, but this has been postponed for v0.4 to ensure that there was a underlying stable release of PySLM as reference to ensure users can utilise the library without waiting for the support structure element to stabilise.

A summary of notable features amongst fixes are as follows:

  • Added class geometry.utils.ModelValidator with functions to validates the inputs (models, layers) are consistent and coherent prior to exporting to machine build files using libSLM.
  • Added an alternative method BaseHatcher.clipContourLines for clipping a list of contour scan vectors. See the previous post about generating custom sinusoidal scan strategy using this method.
  • Added method hatching.simplifyBoundaries to simplify boundaries using Sci-kit Image method based on Douglas-Peucker algorithm.
  • Added a methodvisualise.visualiseOverhang to visualise overhangs – in preparation for support structure analysis
  • Added function argument index to visualise.plot in order to visualise the scan vector parameters (e.g. length, laser parameters, build style id)

Any requests for additional features or other improvements feel free to get in touch.

Custom Scan Strategies in SLM / L-PBF with PySLM: Sinusoidal Scanning

Additive Manufacturing Blog L-PBF PySLM No Comments

Building upon the previous post that provided a detailed breakdown for creating custom island scan strategies, this further post documents a method for deploying custom ‘hatch’ infills. This is particularly desirable capability sought by researchers and has been touched upon very little in the current research. The use of unit-cell infills or in particular fractal filling curves such as the Hilbert curve have been sought for better controlling the thermal history and melt pool stability of hatch infills.

This has been previously explored in SLS [1]][2] and in SLM on a previous collaborators at the University of Nottingham investigating Fractal scanning strategy [3][4].

Typically, hatch infills are sequences of linear lines that form the the ‘hatch’ pattern. Practically, these are very efficient mechanism for infilling a 2D area by using 1D line elements when rastering a laser. Clipping of lines within polygons is intuitive. As discussed there are various scan strategies that can be employed to generate variations on this infill – i.e. stripe, checkerboard/island scan strategy and also modifying the order or sorting of the hatch vectors.

Geometrical scan strategies that adapt the infill based on the underlying geometry, i.e. lattices are acknowledges as ways for drastically improving the performance and the quality of these characteristic structures. This would be based on some medial-axis approach. This post will not specifically delve into this, rather, demonstrate an approach for custom infills on bulk regions.

Ultimately, drastically changing the behavior of the underlying hatch infill has not really been explored. This post will demonstrate an example that could be employed and explored as part of future research.

Custom Sinusoidal Approach

Sinusoidal scanning has been employed in welding research [5] and also in direct energy deposition (DED) [6][7][8] in order to improve the stability and quality of the joining or manufacturing process.

The process of generating this particular scan strategy requires some careful thought to improve the efficiency of the generation, especially given the overall increase in number of points require to essentially ‘sample’ across the sin curve.

The implementation requires subclassing the Hatcher class, by re-implementing the BaseHatcher.generateHatching and the BaseHatcher.hatch methods.

Unlike, the normal hatch vectors, the sinusoidal pattern has to be treated as a series of connected line segments, without any jumping. This requires using the ContourGeometry representation to efficiently store the discretised curve. As a result, the Hatcher.hatch method has to be re-implemented to take account of this.

The procedure builds upon previous methods to define customer behavior (see previous post). The first steps are to define a local coordinate system x' and y' for generating the individual sin curve. A sine curve y' = A \sin(k x') is generated to fill the region bounding box accordingly, given a frequency and amplitude parameter along x'.

The number of points used to discretise the sine curve is determined by \delta x. This needs to be chosen to suit the parameters for the periodicity and amplitude of the sine curve. A reasonable compromise is require as this will severely impact both the performance of clipping these curves, but also the overall file size of the build file generated.

dx = self._discretisation # num points per mm
numPoints = 2*bboxRadius * dx

x = np.arange(-bboxRadius, bboxRadius, hatchSpacing, dtype=np.float32).reshape(-1, 1)
hatches = x.copy()

"""
Generate the sinusoidal curve along the local coordinate system x' and y'. These will be later tiled and then
transformed across the entire coordinate space.
"""
xDash = np.linspace(-bboxRadius, bboxRadius, int(numPoints))
yDash = self._amplitude * np.sin(2.0*np.pi * self._frequency * xDash)

"""
We replicate and transform the sine curve along adjacent paths and transform along the y-direction
"""
y = np.tile(yDash, [x.shape[0], 1])
y += x

x = np.tile(xDash, [x.shape[0],1]).flatten()
y = y.ravel()

After generating single sine curve, numpy.tile is used to efficiently replicate the curve to fill the entire bounding box region. Each curve is then translated by an increment defined by x, to represent the effective hatch spacing or hatch distance.

The next important step is to define the sort order for scanning these. This is slightly different, in that the sort order is done per line segment used to discretise the curve. This is subtle, but very important because this ensures that the curves when clipped by the slice boundary are scanned in the same prescribed sequential order.

The increment of 1\times10^5 is used in order to potentially differentiate each curve later, if required.

# Seperate the z-order index per group
inc = np.arange(0, 10000*(xDash.shape[0]), 10000).astype(np.int64).reshape(-1,1)
zInc = np.tile(inc, [1,hatches.shape[0]]).flatten()
z += zInc

coords = np.hstack([x.reshape(-1, 1),
                    y.reshape(-1, 1),
                    z.reshape(-1, 1)])

Following the generation of these sinusoidal curves, a transformation matrix is applied accordingly, before these are clipped in the Hatcher.hatch method.

The next crucial difference, that has been implemented from PySLM version 0.3, is a new clipping method, BaseHatcher.clipContourLines. The following method is different from BaseHatcher.clipLines, in that clips ContourGeometry separately. This is important for keeping the scan vectors separate and in the correct order, which would be otherwise difficult to achieve. The clipped results are implicitly separated into contour geometry groups.

hatches = self.generateHatching(paths, self._hatchDistance, layerHatchAngle)

clippedPaths = self.clipContourLines(paths, hatches)

# Merge the lines together
if len(clippedPaths) > 0:
    for path in clippedPaths:
        clippedLines = np.vstack(path) 
        
        clippedLines = clippedLines[:,:2]
        contourGeom = ContourGeometry()

        contourGeom.coords = clippedLines.reshape(-1, 2)

        layer.geometry.append(contourGeom)

The next step is to sort the clipped paths into the right order. This is done by using the 1st value of 3rd index column accordingly sorting using sorted with a lambda function.

"""
Sort the sinusoidal vectors based on the 1st coordinate's sort id (column 3). This only sorts individual paths
rather than the contours internally.            
"""
clippedPaths = sorted(clippedPaths, key=lambda x: x[0][2])

Now, the result of the sinusoidal scan strategy can be visualised below.

Sinusoidal Hatch Scan Strategy for Selective Laser Melting - PySLM
Sinusoidal Hatch Scan Strategy for Selective Laser Melting – PySLM

This approach currently is very intensive to generate during the clipping operation, due to the number of edges along each clipping operation. Using the previous techniques with the island scan strategy in a previous post, could be use to amorotise a lot of the cost of clipping.

Example Script

The script is available on github at examples/example_custom_sinusoidal_scanning.py

References

References
↑1 Yang, J., Bin, H., Zhang, X., & Liu, Z. (2003). Fractal scanning path generation and control system for selective laser sintering (SLS). International Journal of Machine Tools and Manufacture, 43(3), 293–300. https://doi.org/10.1016/S0890-6955(02)00212-2
↑2 Ma, L., & Bin, H. (2006). Temperature and stress analysis and simulation in fractal scanning-based laser sintering. The International Journal of Advanced Manufacturing Technology, 34(9–10), 898–903. https://doi.org/10.1007/s00170-006-0665-5
↑3 Catchpole-Smith, S., Aboulkhair, N., Parry, L., Tuck, C., Ashcroft, I. A., & Clare, A. (2017). Fractal scan strategies for selective laser melting of ‘unweldable’ nickel superalloys. Additive Manufacturing, 15, 113–122. https://doi.org/10.1016/j.addma.2017.02.002
↑4 Sebastian, R., Catchpole-Smith, S., Simonelli, M., Rushworth, A., Chen, H., & Clare, A. (2020). ‘Unit cell’ type scan strategies for powder bed fusion: The Hilbert fractal. Additive Manufacturing, 36(July), 101588. https://doi.org/10.1016/j.addma.2020.101588
↑5 Tongtong Liu, Zhongyan Mu, Renzhi Hu, Shengyong Pang,
Sinusoidal oscillating laser welding of 7075 aluminum alloy: Hydrodynamics, porosity formation and optimization, International Journal of Heat and Mass Transfer, Volume 140, 2019, Pages 346-358, ISSN 0017-9310, https://doi.org/10.1016/j.ijheatmasstransfer.2019.05.111
↑6 Cao, Y., Zhu, S., Liang, X., & Wang, W. (2011). Overlapping model of beads and curve fitting of bead section for rapid manufacturing by robotic MAG welding process. Robotics and Computer-Integrated Manufacturing, 27(3), 641–645. https://doi.org/10.1016/j.rcim.2010.11.002
↑7 Zhang, W., Tong, M., & Harrison, N. M. (2020). Scanning strategies effect on temperature, residual stress and deformation by multi-laser beam powder bed fusion manufacturing. Additive Manufacturing, 36(June), 101507. https://doi.org/10.1016/j.addma.2020.101507
↑8 Ding, D., Pan, Z., Cuiuri, D., & Li, H. (2015). A multi-bead overlapping model for robotic wire and arc additive manufacturing (WAAM). Robotics and Computer-Integrated Manufacturing, 31, 101–110. https://doi.org/10.1016/j.rcim.2014.08.008

Proudly powered by WordPress & Skyrocket Themes

MENU

Navigation